Parent Functions

In the realm of mathematics, particularly within the field of algebra and calculus, lies a fundamental concept known as parent functions. These functions serve as the building blocks upon which more complex functions are constructed and understood. In this exploration, we delve into the essence of parent functions, their characteristics, and their significance in mathematical analysis.

Table of Contents

Understanding Parent Functions:

Parent functions are the most basic functions that serve as prototypes for a family of functions. They provide a template or a blueprint from which other functions can be derived through various transformations such as translations, reflections, stretches, and compressions. These transformations alter the parent function’s shape, size, and position while preserving its essential properties.

Common Parent Functions:

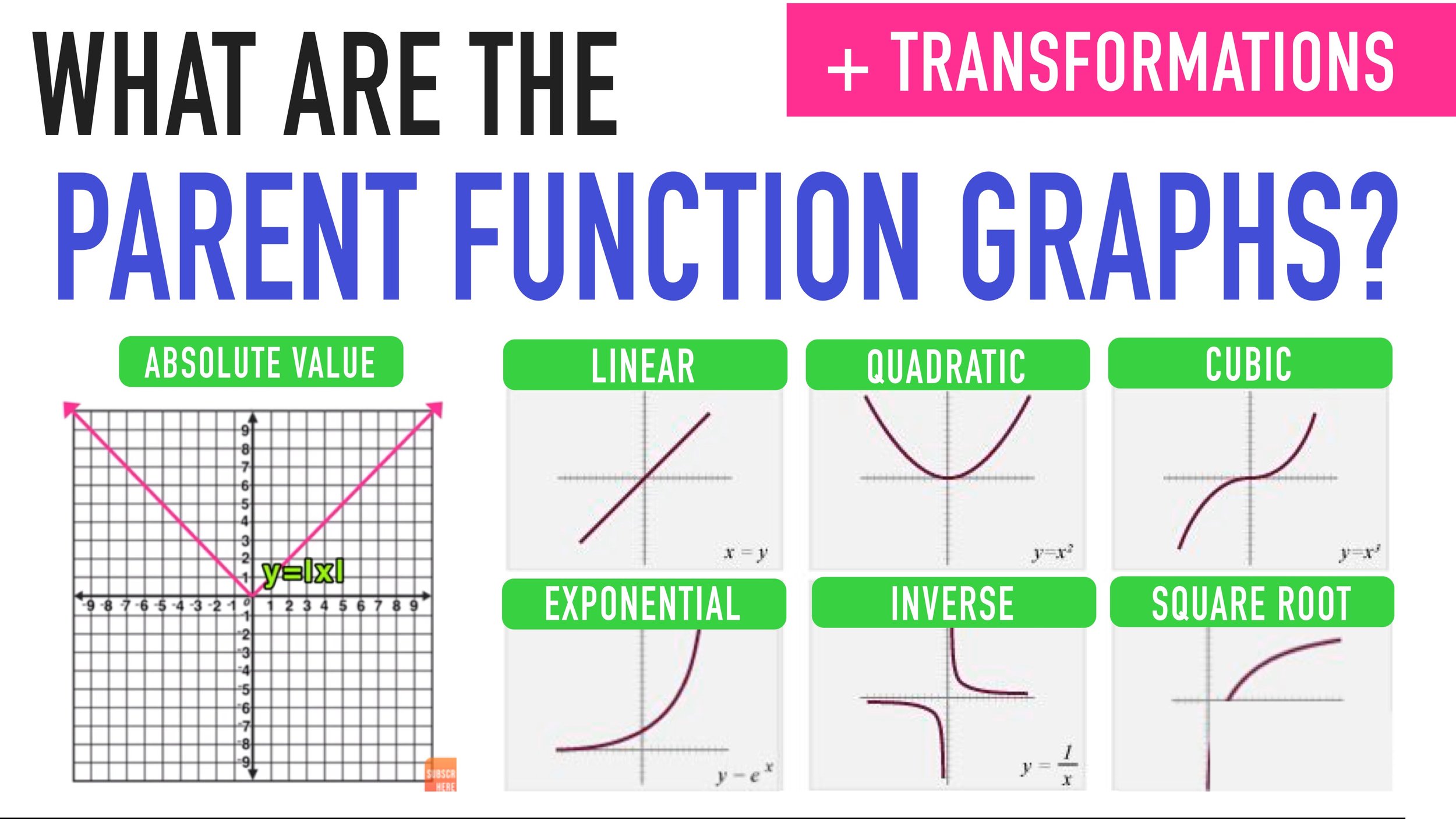
Several fundamental parent functions play pivotal roles in mathematics. These include linear functions, quadratic functions, cubic functions, square root functions, absolute value functions, exponential functions, and logarithmic functions. Each of these functions exhibits distinct characteristics that define its behavior and graphical representation.

1. Linear Function (f(x) = mx + b): The linear function is perhaps the simplest of all parent functions. It represents a straight line with a constant rate of change (slope) and a y-intercept (where the line intersects the y-axis). Its general form is expressed as f(x) = mx + b, where ‘m’ represents the slope and ‘b’ represents the y-intercept.

2. Quadratic Function (f(x) = ax² + bx + c): Quadratic functions are characterized by the presence of a squared term (x²). They form parabolic curves and are widely used to model various real-world phenomena. The general form of a quadratic function is f(x) = ax² + bx + c, where ‘a’, ‘b’, and ‘c’ are constants, and ‘a’ determines the direction and width of the parabola.

3. Cubic Function (f(x) = ax³ + bx² + cx + d): Cubic functions involve terms up to the power of three (x³). They exhibit more complex behavior, often featuring two points of inflection. Cubic functions are essential in modeling situations where growth or decay is nonlinear and can be expressed in the form f(x) = ax³ + bx² + cx + d.

4. Square Root Function (f(x) = √x): The square root function represents the inverse operation of squaring a number. It produces a curve that starts at the origin and gradually increases, never falling below the x-axis. The square root function is denoted as f(x) = √x and is defined only for non-negative real numbers.

5. Absolute Value Function (f(x) = |x|): The absolute value function yields the distance of a number from zero on the number line. It produces a V-shaped graph symmetric about the y-axis. The function f(x) = |x| returns the absolute value of x, ensuring that the output is always non-negative.

6. Exponential Function (f(x) = a^x): Exponential functions involve a constant base raised to the power of a variable exponent. They exhibit rapid growth or decay depending on whether the base is greater or less than one. The general form of an exponential function is f(x) = a^x, where ‘a’ is the base.

7. Logarithmic Function (f(x) = logₐ(x)): Logarithmic functions are the inverse of exponential functions. They express the power to which a base (denoted by ‘a’) must be raised to produce a given value. Logarithmic functions are typically written as f(x) = logₐ(x), where ‘x’ is the argument and ‘a’ is the base.

Significance of Parent Functions:

Parent functions serve as the cornerstone of mathematical analysis and modeling. They provide a framework for understanding more complex functions by identifying common patterns and behaviors. Moreover, studying parent functions enables mathematicians and scientists to formulate equations that accurately describe natural phenomena, economic trends, and various scientific processes.

Applications in Real-World Scenarios:

The concepts of parent functions find widespread applications across diverse fields:

Physics: In physics, parent functions are used to model the motion of objects, the propagation of waves, and the behavior of systems under various forces.
Engineering: Engineers utilize parent functions to design structures, optimize processes, and analyze data in fields such as civil engineering, electrical engineering, and mechanical engineering.
Economics: Economists employ parent functions to study supply and demand curves, analyze market trends, and forecast economic indicators.
Biology: Biologists use parent functions to model population growth, enzyme kinetics, and physiological processes within organisms.

Conclusion:

Parent functions serve as the foundational elements upon which mathematical analysis and modeling are built. By understanding the characteristics and behaviors of these fundamental functions, mathematicians and scientists gain insights into the complex phenomena observed in the natural world. Whether in physics, engineering, economics, or biology, the study of parent functions remains essential for unraveling the mysteries of our universe and developing solutions to real-world problems.