P in NP

In the realm of computer science, few questions are as enigmatic and tantalizing as the P vs. NP problem. At its core, it probes the very essence of computation, challenging us to discern the boundary between what is feasibly solvable and what lies beyond the realm of efficient algorithms. This enduring enigma has captivated mathematicians, computer scientists, and enthusiasts alike for decades, prompting intense scrutiny and spawning a plethora of conjectures and theories.

Defining P and NP:

Before delving into the intricacies of the P vs. NP problem, it’s essential to understand the fundamental concepts of P and NP.

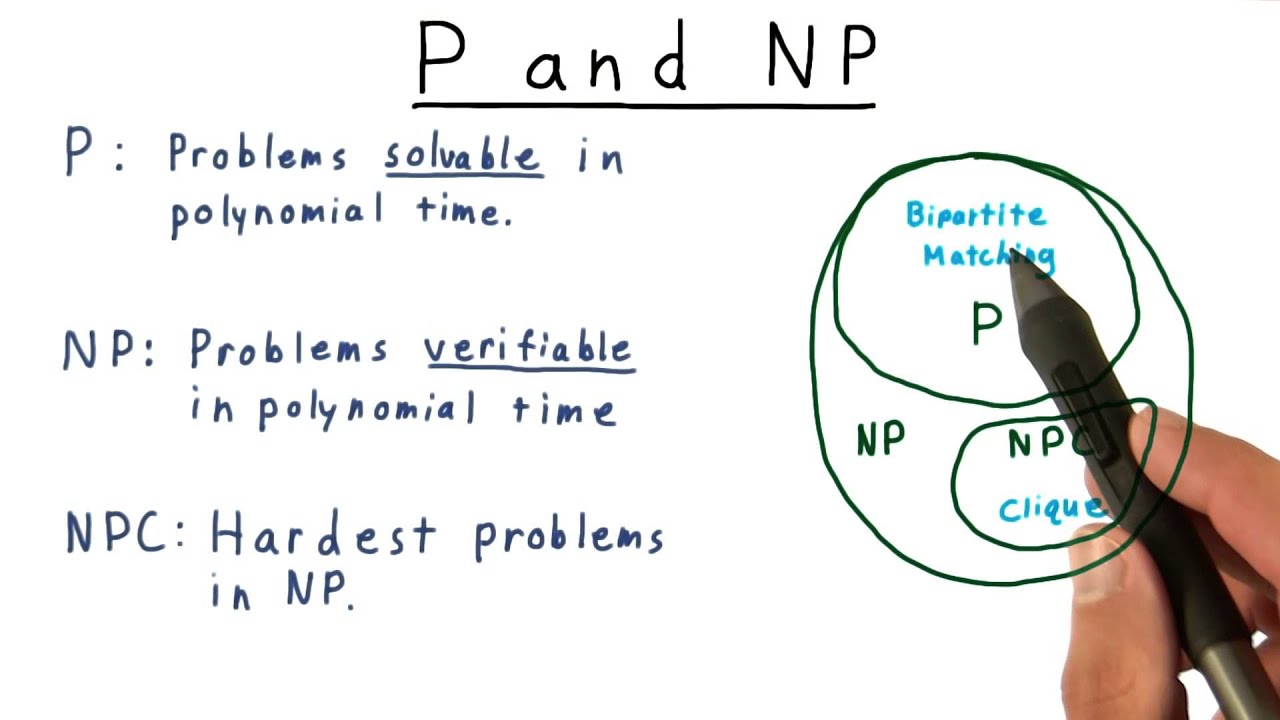
P (Polynomial Time): This class encompasses decision problems that can be solved by a deterministic Turing machine in polynomial time, meaning the time taken to solve the problem grows polynomially with the size of the input. In simpler terms, algorithms belonging to class P are efficiently solvable.

NP (Nondeterministic Polynomial Time): NP, on the other hand, comprises decision problems for which a potential solution can be verified in polynomial time. While NP problems might be challenging to solve outright, if presented with a purported solution, one can efficiently verify its correctness. Examples of NP problems include the traveling salesman problem and the Boolean satisfiability problem.

The P vs. NP Conundrum:

The crux of the P vs. NP problem lies in determining whether every problem in NP is also in P, or more succinctly, whether P equals NP. In simpler terms, does the ability to quickly verify a solution imply the existence of an equally swift algorithm for finding it?

Resolving this question has profound implications across various domains, particularly in cryptography, optimization, and algorithmic efficiency. A proof that P equals NP would signify that problems once thought to be computationally intractable could indeed be solved efficiently, revolutionizing fields such as cryptography by rendering many encryption methods vulnerable to rapid decryption.

However, the prospect of P equaling NP remains elusive, with the majority of researchers leaning towards the belief that P ≠ NP. This assertion is supported by the plethora of NP-complete problems, which are considered among the most challenging computational conundrums, defying attempts at efficient solutions.

NP-Complete Problems:

Central to the discourse surrounding P vs. NP are NP-complete problems. These are a subset of NP problems with the distinctive property that any problem within NP can be transformed into an instance of an NP-complete problem in polynomial time.

The Traveling Salesman Problem (TSP): One of the most renowned NP-complete problems, the TSP involves finding the shortest possible route that visits each city in a given list exactly once and returns to the original city. Despite its seemingly simple formulation, the combinatorial explosion of possible routes makes finding the optimal solution an arduous task.

The Boolean Satisfiability Problem (SAT): Another quintessential NP-complete problem, SAT revolves around determining whether there exists an assignment of truth values to variables in a Boolean expression such that the entire expression evaluates to true. Despite its simplicity in description, SAT’s computational complexity escalates rapidly with the size of the expression.

The Quest for Resolution:

Despite decades of intensive research and exploration, the P vs. NP problem remains unresolved. Various approaches, ranging from combinatorial techniques to sophisticated mathematical formulations, have been employed in attempts to shed light on this tantalizing puzzle.

Complexity Theory: Central to the quest for understanding P vs. NP is complexity theory, which provides the foundational framework for analyzing the computational difficulty of problems. Through the classification of problems into complexity classes such as P, NP, and NP-complete, complexity theory offers invaluable insights into the inherent intricacies of computational tasks.

Proof Techniques: Researchers have employed a myriad of proof techniques in their endeavors to tackle the P vs. NP problem. From diagonalization arguments to probabilistic methods, each approach offers a unique perspective on the fundamental nature of computational complexity. Despite numerous promising leads, a definitive resolution remains elusive.

Implications and Applications:

The resolution of the P vs. NP problem carries profound implications across various domains of science and technology.

Cryptography: A proof that P equals NP would upend the foundations of modern cryptography, rendering many cryptographic schemes vulnerable to rapid decryption. This would necessitate a paradigm shift in cryptographic protocols and encryption methods, sparking a new era of secure communication.

Optimization: Efficiently solving NP-complete problems could revolutionize optimization processes across diverse fields, from logistics and resource allocation to scheduling and manufacturing. The ability to swiftly find optimal solutions would enhance productivity and streamline operations in numerous industries.

Algorithmic Efficiency: Resolving P vs. NP would provide invaluable insights into the inherent complexity of computational tasks, guiding the development of more efficient algorithms and computational techniques. This, in turn, could accelerate advancements in artificial intelligence, data analysis, and scientific computing.

Conclusion:

The P vs. NP problem stands as one of the most profound and enduring enigmas in computer science, challenging our understanding of compmplexity and algorithmic efficiency. utational coWhile the quest for resolution continues unabated, fueled by the ingenuity and perseverance of researchers worldwide, definitive answers remain elusive. Whether P equals NP or not, the pursuit of clarity in this realm has catalyzed advancements across various disciplines, underscoring the profound interplay between theory and practice in the ever-evolving landscape of computation.